Wins and Runs and Linear Regression

I hope I didn’t lose you at the end of that title. Statistics can be confusing and boring. But at least you’re just reading this and not trying to learn the subject in your spare time like yours truly. When you work with data you try to look for relationships or patterns to help tell a story. Linear regression is a topic that I’ve been quite interested in and hoping to incorporate into analyzing sports data.

I asked ChatGPT to explain linear regression to me like a five-year-old and this is what I got:

“Linear regression is a tool that helps us understand how things are related to each other. It's like when you play with blocks, and you notice that when you add more blocks, your tower gets taller. Linear regression helps us figure out how much taller your tower will get for each extra block you add.”

That works for me. In chapter 4 of Analyzing Baseball Data with R¹, the authors investigate the relationship between runs and wins. It’s easy to assume the teams who score a lot of runs should have a high winning percentage, but is that case? So, like our innocent artificial intelligent produced example above, let’s see how tall our towers get with each block added.

Below are the scripts that I used to carry out this analysis. I have slightly changed them from the book. We will be looking at data since the 2010 season while excluding the 2020 Covid shortened season.

First, we open the libraries we need to work with. We will use tidyverse and Lahman. Lahman is a baseball database with data going all the way back to the 1871 season.

library(tidyverse)
library(Lahman)

Now we need to filter out all of the data we do not need and create a data frame to work with going forward.

#my_teams will be the data frame and we are creating by filtering off the Teams table in the Lahman database

my_teams <- Teams %>% filter(yearID > 2010 & yearID != 2020) %>% select(teamID, yearID, lgID, G,W,L,R,RA)

#we exclude the 2020 season by using operator "!="

Let’s take a look at what we have so far. Using the “tail” function, we are looking at the bottom six rows of the table. You will see that we have the G (games), W (wins), L (losses), R (runs), and RA (runs allowed) columns that we pulled in the previous line of code.

tail(my_teams) 

   teamID yearID lgID   G   W   L   R  RA
295    SFN   2021   NL 162 107  55 804 594
296    SLN   2021   NL 162  90  72 706 672
297    TBA   2021   AL 162 100  62 857 651
298    TEX   2021   AL 162  60 102 625 815
299    TOR   2021   AL 162  91  71 846 663
300    WAS   2021   NL 162  65  97 724 820

In order to find the relationship between runs and wins we need to be able to calculate a run differential that will give us the difference between runs scored and runs allowed. Now we will create two new variables, run differential and winning percentage, for the data frame “my_teams” using the mutate() function.

#we use simple arithmetic to calculate these new variables
#RD is runs scored minus runs allowed
#winning percentage is wins divided wins plus losses

my_teams <- my_teams %>% mutate(RD = R - RA, Wpct = W / (W + L))

Let’s create a scatterplot to see if there’s a relationship between run differential and winning percentage.

#We use a package in tidyverse called ggplot that we can create plots with
#Let's put RD on the x axis and Winning % on the y axis and give them titles

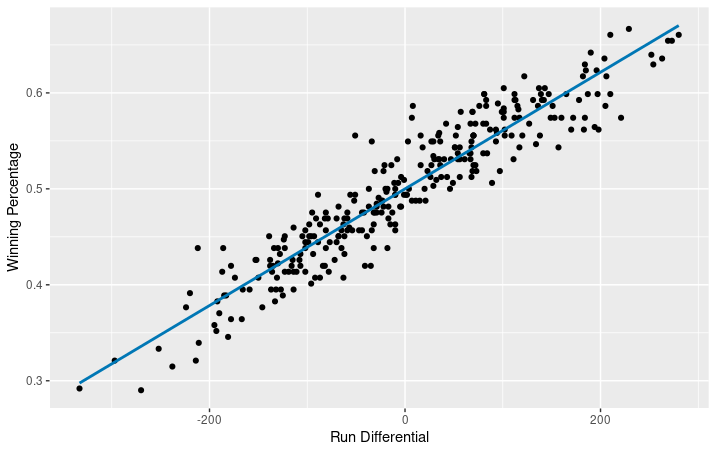
run_diff <- ggplot(my_teams, aes(x = RD, y = Wpct)) + geom_point() + scale_x_continuous("Run Differential") + scale_y_continuous("Winning Percentage")

#Now we can add a blue line to show a better representation of the correlation 
run_diff + geom_smooth(method = "lm", se = FALSE, color =  crcblue)

Look at that. We have a positive correlation between run differential and winning percentage in our data frame. This shows us that if you have a great run differential, then you probably have a pretty high winning percentage. Now it’s time to dive a little bit deeper and discuss linear regression.

By applying a linear regression model, it is possible to make predictions about a team’s winning percentage using the number of runs they scored and allowed over the course of a season. Winning percentage is our dependent variable because that is what we are trying to predict and the variables that come after the equals sign are our independent variables. Independent variables (RD in our example) are used to predict dependent variables. The coefficients a and b represent the intercept and the slope of the regression line, respectively, and e is the error term or residual, which represents the unexplained variability in the dependent variable.

Wpct = a + b x RD + e

What is so great about R is that you can use a built-in linear model function (lm) seen below.

linfit <- lm(Wpct ~ RD, data = my_teams)
linfit

Call:
lm(formula = Wpct ~ RD, data = my_teams)

Coefficients:
(Intercept)           RD  
  0.4999867    0.0006079  

This translates to Wpct = 0.4999867 + 0.0006079 x RD. What this means is that a team with a RD of zero will win half of its games given that the estimated intercept = 50% or .500. So, to harken back to our 5-year-old explanation of how tall the tower will get with each block. This says that that with every unit increase there will be a corresponding increase of winning percentage by 0.0006079. If a team scored 725 runs and allowed 725 runs, then it would predict to win half of its games (record of 81-81). If a team scored 740 runs and allowed 720 then they would have a run differential of +20 and be predicted to have a winning percentage of 0.500 + 20 x 0.0006079 = 0.512.

The scatterplot below shows four teams that had the largest residuals in the data frame. The 2021 Seattle Mariners had a run differential of -51 and should have had a winning percentage of 0.469 but instead finished with a winning percentage of 0.556. Their residual value is 0.556 - 0.469 = 0.087 or 0.087 x 162 = 14.1 games.

Regarding the example of the 2021 Seattle Mariners, their residual value of 0.087 indicates that their actual winning percentage was 0.087 higher than what would have been expected based on their run differential. This means that they won more games than what would have been predicted based on their performance, resulting in a positive residual value. The calculation of 0.087 x 162 = 14.1 games represents the number of additional games that the Mariners won beyond what would have been expected based on their run differential. They could have used a couple extra wins seeing that they finished 5 games behind the Houston Astros in the NL West and only 2 games out of the second American League Wild Card spot. This would culminate in their 20th straight season of missing the playoffs. Fortunately for them, 2022 would lead them back to October baseball where they finished 90-72. The same record they had in 2021. Baseball is funny.

Sources:

Analyzing Baseball Data with R | Exploring Baseball Data with R (wordpress.com)

1. Marchi, M., Albert, J., & Baumer, B. (2018). Analyzing Baseball Data with R (2nd ed.). Chapman and Hall/CRC.